Scenario Analysis

Volatility-coordinated scenarios explore simultaneous shocks to market price and volatility. Because the change to volatility is a deterministic function of the price change, the coordinated scenarios still only explore a one-dimensional subspace of the very large space of possible market outcomes.

Volatility Term Structure Response

One common feature of the coordinated scenarios is that the volatility shock is not applied directly to implied volatility or to volatility products. Instead, it is first multiplied by a term-structure response function, which we will denote as VR(t) where t is the time to option expiry (for stock options) or to futures delivery (for volatility index derivatives). To reflect the observed propensity of volatility levels to fluctuate less as this time increases, VR(t) is a decreasing function with VR(0) = 1.

ETFs and ETNs which invest in volatility index derivatives do not use any single future, but must roll their portfolios through time. Thus we cannot use VR(t) directly for them; instead we use the measured historical beta of the ETF/ETN with respect to the underlying volatility index (e.g., the beta of VXX with respect to VIX). These historical betas are updated daily.

We refer to the volatility change before application of VR(t) or beta as the "nominal" change.

Equity Markets

For equity products and equity-derived volatility products, we use the formula

Y = -X when X>0, -10*x when X<0

to derive the nominal volatility shock "Y" from the price shock "X". For example, a 30% increase in market prices is accompanied by a 30% nominal decrease in volatility; a 20% decrease in market prices is accompanied by a 200% nominal increase in volatility. As always, this functional relationship is not predictive of real-world changes.

In the resulting scenarios, the value computation for a market instrument depends on its type. The table below gives a few representative examples:

Note: The volatilities of volatility products are not changed in these scenarios.

Floor on VIX

There is also a caveat to the above: we impose a lower limit on the value of Y, in order to create a lower limit on the values of the spot VIX index which will be explored by the scenarios. Thus the scenarios presented in Risk Navigator embed this assumption about VIX behavior. In a large real-world market move, this assumption could turn out to be incorrect. See samples by clicking the drop-down menu below.

As illustrated in the below image, our sample portfolio contains both stock and volatility instruments. The latter are grouped under "SPX" in the examples, since their value is ultimately derived from SPX volatility.

P/L by Market Price Change

Risk Navigator supports scenarios with coordinated volatility, and also with no volatility change. The results can be quite different:

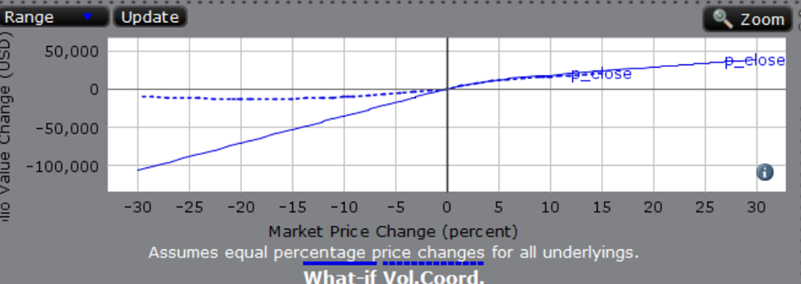
Since the price-based part of the portfolio is a short covered call and an outright long position, it loses value as market prices drop. This is reflected in the "What-if" line on the graph, which shows the price-based instruments losing value and the vol-based instruments unchanged.

The vol-based part of the portfolio contains long positions in VXX stock, a VXX call, and a VIX future, all of which will profit from a volatility increase. If a market price drop is accompanied by a volatility increase, then the vol-based instruments will gain value in these market-down scenarios. The "Vol.Coord." line on the graph shows a smaller P&L change, due to this offsetting effect.

It is important to note that such simple scenarios cannot be expected to quantitatively predict the details of a large market move. Both curves are computed from vastly simplified toy models of what might happen in a severe market downturn. Their only goal is to compactly summarize one aspect of a portfolio's potential behavior.

P/L by Equity Market Volatility Change

The graph on the Volatility Products tab shows the results of the same volatility-coordinated scenario analysis as that used on the Equity tab.

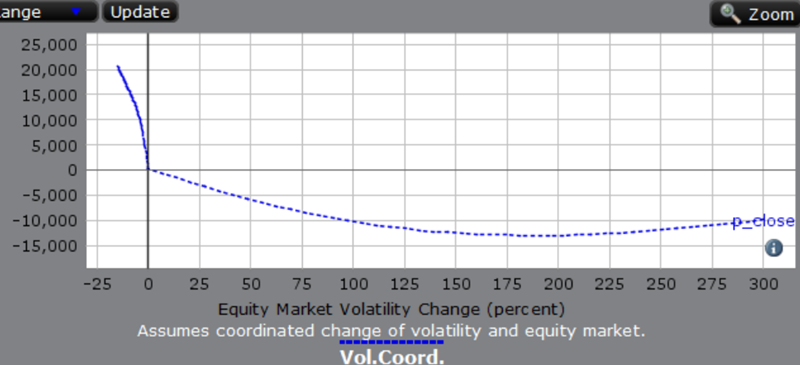
However, the graph's x-axis is now the volatility change rather than the corresponding price change. Because the volatility-coordinated scenarios associate increasing price and decreasing volatility, the direction of P&L change appears to have reversed. And because the relationship between market price change and volatility change is non-linear, the graph's shape appears to have changed.

The values in the two graphs nonetheless correspond precisely. For instance, a single scenario in which prices increase 10% and nominal volatilities decrease 10% contributes one point on each graph:

• The point where "Market Price Change (percent)" is 10, on the Equity tab

• The point where "Equity Market Volatility Change (percent)" is -10, on the Volatility Products tab

Another scenario, in which prices decrease 20% and nominal volatilities increase 200%, contributes a different point:

• The point where "Market Price Change (percent)" is -20, on the Equity tab

• The point where "Equity Market Volatility Change (percent)" is 200, on the Volatility Products tab

In scenarios like the latter, the volatility products will experience a positive P&L; but because the volatility increase is assumed to be accompanied by a decline in market prices, the price-based products will experience a negative P&L in the same scenario. The graph shows the sum of these two effects.

The Portfolio Relative P&L graph illustrates how the total value of your portfolio for a specific asset class (or a subset of your portfolio) will change, based on a percent change in the price(s) of the underlying(s). Available settings may change based on the asset class displayed.

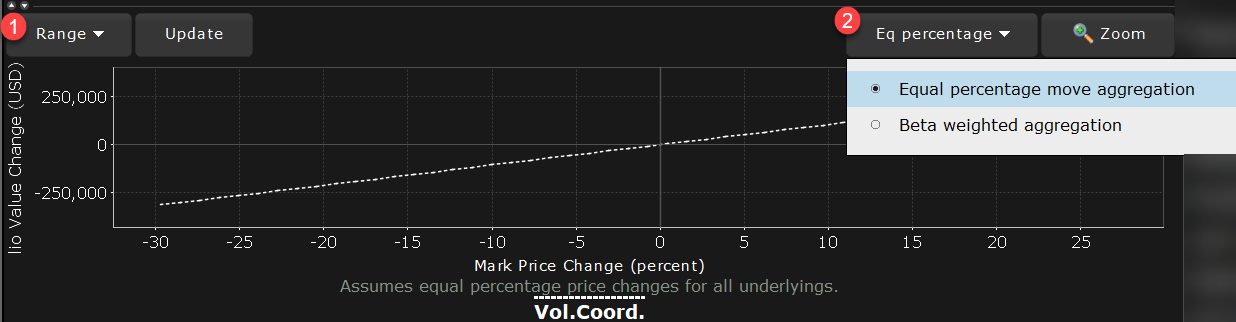
1 - Change the range for the underlying price change shown on the horizontal axis. The default value is +/- 30%.

2 - Change plot aggregation when Beta Weighted Portfolio is enabled (from View menu)

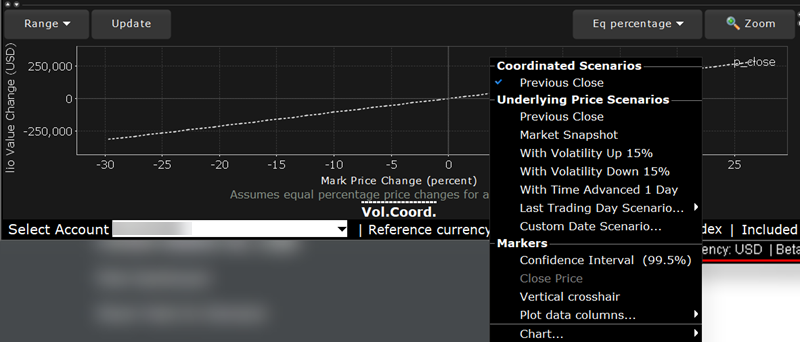
Use the right-click menu to create date scenarios, add or remove time and volume variables, enable the vertical crosshair and set data column slicers.

The image above shows the portfolio relative P&L for an equity portfolio, based on the value All Underlyings selected from the Underlying list in the Report Selector.

For a single underlying, you can toggle between showing the absolute price or showing the underlying price change as a percent. Click the price label below the horizontal price axis to select a display type.

Note that for leveraged ETFs, the Risk Navigator moves them by their target performance ratio in the aggregated P&L graph. For example, for an index and its triple inverse ETF, to the +10% P&L it adds the index P&L at 10% to the ETF P&L at -30%. When either one is plotted individually, it shows their own P&L, but it shows the index on a +/-30% range and the ETF on a +/-90% range.

Beta analysis in IBKR Risk Navigator allows the investor to view the P&L plot differently. In its default format "Equal Percentage," the P&L plot assumes a same percentage move for all underlying portfolio pieces. When Beta Weighted Aggregation is selected, the underlying price scenario includes beta weighted price changes. Beta explains the performance of a stock over and above that associated only with the performance of the market itself.

The Confidence Interval, shown within the yellow vertical lines, illustrates the worst-case loss over a one-day period with a default 99.5% confidence level. Use the Confidence sub-command on the Settings menu to toggle between 95%, 99% and 99.5% confidence levels. Turn the Confidence Level brackets on or off using the Confidence Interval command on the right-click menu.

For portfolios containing options or volatility products (like VIX or its derivatives), vol-coordinated price changes show the effect of a change in market price level and a corresponding simultaneous change in volatility level. In scenarios where stock prices are down X%, vols are assumed to simultaneously increase by up to (10*X)% for short-dated options, decaying gradually to (2*X)% for options with longer expiries. Conversely, in scenarios with stock prices up X%, vols are assumed to be down X% for short-dated options, decaying to (X/5)% for longer expiries.

Curves generated using these coordinated volatility changes will be marked "Vol.Coord.", and will be displayed together with a tool tip detailing the scenarios used.

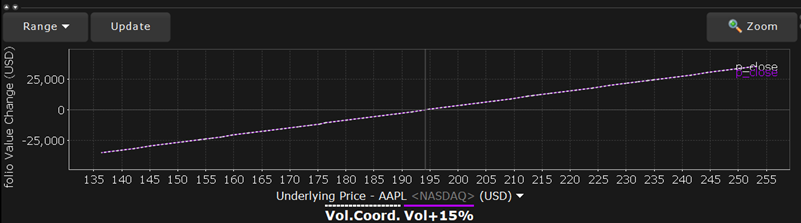
Use the Vol-up by 15%*, Vol-down by 15%* and reduced time to expiry by 1 day checkboxes in the right-click menu to view the plot under different scenarios to help you visualize the volatility and time risk in your option positions. While you can elect to display the base P&L using both the previous day’s closing price and the most recent dynamic price, the volatility and time variables are always based on the previous close.

*The Vol Up and Vol Down commands increase/decrease projected volatility in relative percent change. Relative percent change is calculated by multiplying the current implied volatility by 15%, and adding/subtracting this value to/from the current implied volatility. For example, if the current implied volatility of an option is 10%, a 15% relative increase would result in an implied volatility of 11.5%, calculated as follows: 10 + (10 * 0.15) = 11.5% . If the current implied volatility of an option is 42.45%, a 15% relative decrease would result in an implied volatility of 36.082%, calculated as follows: 42.45 - (42.45 * 0.15) = 36.082%.

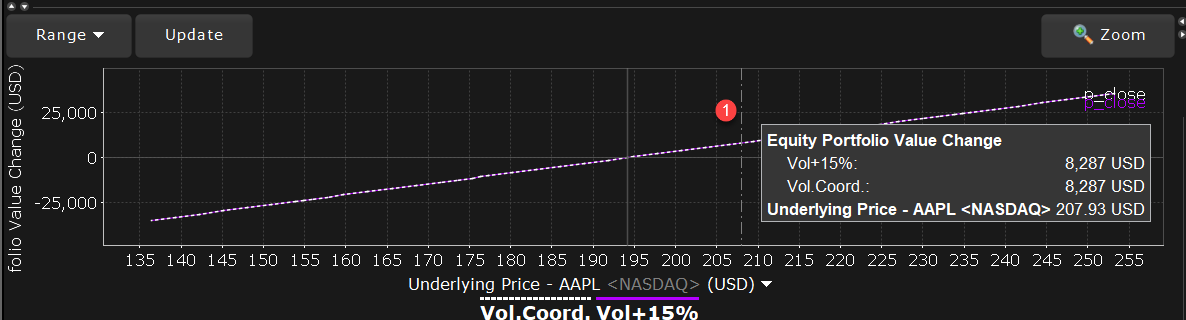
1 - Activate the vertical crosshair from the right-click menu to get mouse-over help at any price-change percentage point.

Note: For Bonds, the P&L plot is based on the interest rate change.

In cases where the index price is invalid for futures/futures options, the graph provides a drop-down selector with available expirations to use for the reference price. Ensure that the "Underlying" field in the report selector has only one contract selected.

Click to view a short video on Risk Navigator P&L and VAR Tabs.

You can elect to modify the variables that affect your risk profile using the Custom scenario command on the View menu. The Custom Scenario section is populated with the same data as the realtime market scenario until you modify the variables.

VAR in the market scenario is calculated based on the previous day's closing price. VAR in the Custom Scenario is calculated based on the current Last price when the scenario is created. Total VAR can be found in the "Value at Risk" report.

To Create a Custom Scenario

1. From the View menu select Custom Scenario.

2. In the Scenario Editor, filter the underlyings you want to include in the custom view.

   • Select All Underlyings to affect the entire portfolio from a single editing line.

   • Select Any Underlyings to edit individual underlyings line by line.

   • Choose a single underlying to show the subportfolio (the underlying and its derivatives). Additionally, use Ctrl + click to select multiple underlyings.

3. Modify the Date to view your risk profile at a future date. By default the date is set to today.

4. In the Underlying Price section, define the value of the price change and the type.

   • ExpV - the Custom Scenario price will be changed to exactly reflect the explicit value in the Price field, either positive or negative depending on the sign. For example, if the price for ABC is currently $60.25 and you enter 55.00 ExpV, the Custom Scenario price for ABC will be $55.00.

   • Chg - Adds or subtracts the value in the Price field, depending on the sign. For example, if the price for ABC is currently $60.25 and you enter -4.25 Chg, the Custom Scenario price for ABC will be $56.00.

   • Chg% - Adds or subtracts the percent of the value in the price field, depending on the sign. For example, if the price for ABC is currently $60.25 and you enter 10 %Chg, the Custom Scenario price for ABC will be $54.23.

     The values in the Custom Scenario are always compared to values in the realtime Market Scenario. For example, if you modify the Price parameter to show a 10% change in the underlying price and get a Custom Scenario price of $54.23, then you modify this price again to see a -10% change, the new calculation will be based on -10% of the market price of $60.25, not the existing custom scenario price of $54.23.

5. Use the Volatility section to modify volatility using the same types (ExpV, Chg and %Chg) as described above in the Price section.

6. Hit Apply at the top left of the Scenario Editor to see the impact of your changes in the Custom Scenario section.

   

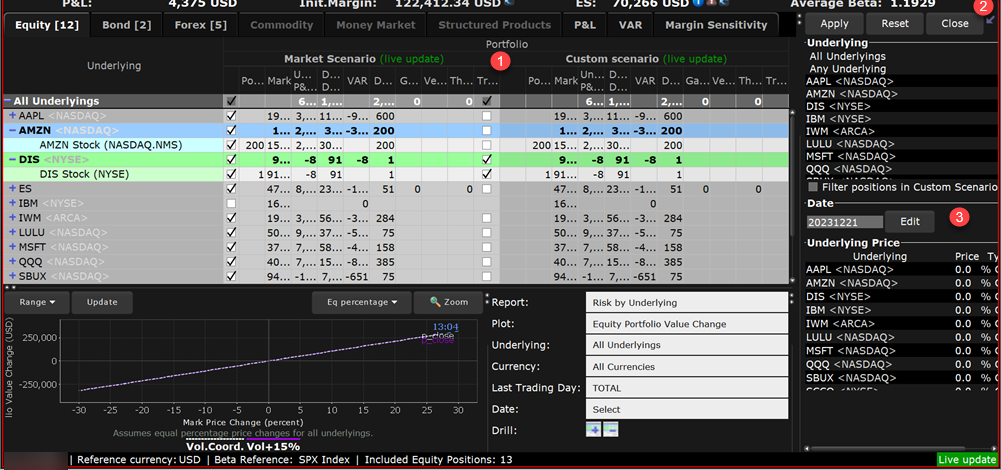
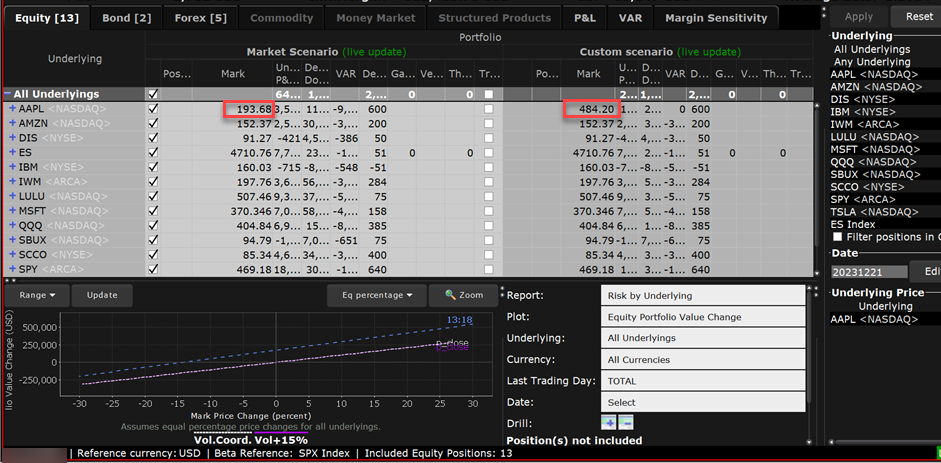
   1 - Side by side market and custom scenarios allows you to easily compare data.

   2 - Toggle the editor to view a full side panel display

   3 - Use the Scenario Editor to change variables that affect the risk status of your portfolio, including date, volatility, and price.

You can create complex custom scenarios by editing the price, date and volatility variables. The examples below are only a few of the possible custom views available, and are meant to help you become familiar with the tool.

Custom Scenario Example 1:

You want to view the impact on your portfolio of a 10% change in the underlying price of IBM.

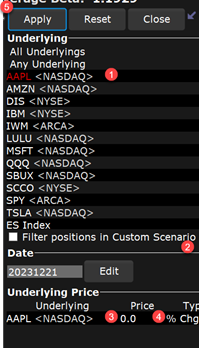
1 - Filter the underlying. In this case, select AAPL.

2 - Optionally check the "Filter positions..." checkbox to hide all values for other underlyings to make the difference between market and custom scenarios easier to see.

3 - Enter the Price value. Be sure to delete the existing value first.

4 - Select the price change type.

5 - Click Apply to see your changes reflected in the Custom Scenario table.

Note: Modified data in the editor appears in red, indicating that you have not yet applied the changes. When you click Apply, the red color is removed.
To remove data changes, click the Reset button at the top of the editor.

The effects of this change can be seen in the Custom Scenario, and can be compared with the real-time market data that appears in the adjoining Market Scenario. The underlying price change shows in the underlying stock line, and the trickle-down affect of this change can be seen in the Price, Value, Delta and Theta fields.